About Dirac
Model
Dirac systems are portable, low power, and room temperature qubit and qudit entropy quantum computers (EQC). A Dirac system solves problems of Objective Function Minimization and Maximization for binary and integer optimization by finding the ground state of a complex system with many intercorrelated variables.
These problems correspond to minimizing or maximizing the expected return of the objective function:
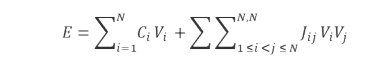
where,
- : the value of each variable; binary and/or integer numbers,
- : the linear coefficient of each variable, which is a real number that can be positive, negative, or zero,
- : the coupling coefficient of two variables, which can be any real number
Principle
Entropy Quantum Computing (EQC) is deeply rooted in the principles of quantum mechanics.
The figure below displays conventional quantum computers limited to nearest neighbor connectivity (left) vs. EQC, which allows all-to-all global connectivity (right):
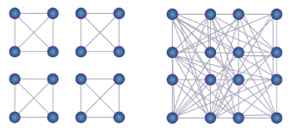
First, loss or decoherence of a quantum state occurs through its coupling to an entropy source with many degrees of freedom (DoF). The apparent diminishing of quantum characteristics as a result is a statistically averaged manifestation of many possible outcomes of such coupling. Second, vacuum is never quiet, and in fact, enormous amounts of random fluctuations occur at all times in each of the vacuum modes. EQC is conceived and developed around these foundational quantum principles. Rather than trying to create and manipulate pristine qubits isolated from the environment, EQC utilizes loss and decoherence, and turns entropy into super-power fuels of its computing engine.
Below provides a visualization of the degrees of freedoms realized through a Dirac system:
 Dimension of Conventional QC vs. Entropy QC
Dimension of Conventional QC vs. Entropy QCCapability
This novel approach of finding the ground state allows global connectivity, instead of limiting connectivities to nearest neighbors. Additionally, by exploiting many DoF of photons, EQC enables superposition of multiple dimensions instead of superpositions of just ‘0’ and ‘1’. Hence, in sharp contrast to other existing quantum platforms, there is no need for cryogenic or isolated housing, and the implementation can use integrated photonics. This leads to the capability to build small size, low power, low cost, scalable, and room temperature entropy quantum computers.